4. Kleisli 圏

ここまでで、型と純粋関数を圏としてモデル化する方法をみてきました。その際に計算効果を持つ非純粋な関数をモデル化するための概念として、モナドが出てきましたね。

ここでは、計算効果の例として、実行内容のログ、トレースを行うことについて考えていきます。モナドの1つの例である Writer、そして Writer の一般化である Kleisli について見ていきましょう。

extension [A](v: Writer[A])
  def map[B](f: A => B): Writer[B] =
    val (logA, resA) = v.run
    Writer(logA, f(resA))

def isEven(n: Int): Writer[Boolean] =
  Writer(
    s"isEven is called with parameter $n. ",
    n % 2 == 0
  )

def isOdd(n: Int): Writer[Boolean] =
  for
    isEvenRes <- isEven(n)
    negateRes <- negate(isEvenRes)
  yield negateRes

isOdd(1)
// res4: Writer[Boolean] = Writer(
//   run = (
//     "isEven is called with parameter 1. negate is called with parameter false. ",
//     true
//   )
// )
isOdd(2)
// res5: Writer[Boolean] = Writer(
//   run = (
//     "isEven is called with parameter 2. negate is called with parameter true. ",
//     false
//   )
// )
Writer("initial log. " -> 3).flatMap(isOdd)
// res6: Writer[Boolean] = Writer(
//   run = (
//     "initial log. isEven is called with parameter 3. negate is called with parameter false. ",
//     true
//   )
// )

これで、通常のロジック (この簡単な例では、奇数か偶数か判定するプログラム) からログの合成については考えなくて良くなりました。各関数は、純粋関数として自分たちのログを出力に入れるだけで良いですね。

実は、今考えたような構造は Writer 圏と呼ばれます。次の節では Writer 圏を定式化していきます。

4.2 Writer 圏

先ほど見たロギング関数の合成の例を圏論の言葉に落とし込むと、Writer 圏というものを考えることができます。

4.2.1 Writer 圏の対象と射

Writer 圏では、先ほど定義したデータ型 Writer を利用します。

この圏では、対象として型を採用し、対象 A から B への射として以下のようにラップされた関数を採用します：

// Writer 圏における射
def f[A, B]: A => Writer[B] = ???

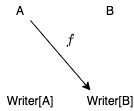
つまり、Writer 圏においては、関数 g: A => B は射ではありません。

2つの関数 negate: Boolean => Writer[Boolean] と isEven: Int => Writer[Boolean] は、Writer 圏における射です。

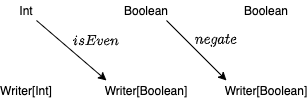
4.2.2 Writer 圏における射の合成

Writer 圏における射の合成は、先ほど定義した flatMap と似たようなものになります。関数 f: A => Writer[B]、関数 g: B => Writer[C] を合成した関数 f >=> g: A => Writer[C] を定義してみましょう。

object Writer:
  def >=>[A, B, C]: (A => Writer[B]) => (B => Writer[C]) => (A => Writer[C]) = f => g => a =>
    val (logF, b) = f(a).run
    val (logG, c) = g(b).run
    Writer((logF + logG), c)

extension [A, B](f: A => Writer[B])
  def >=>[C](g: B => Writer[C]): A => Writer[C] =
    Writer.>=>(f)(g)

>=> 演算は fish 演算子と呼ばれるもので、 andThen や compose と同様、引数で受け取った2つの関数を合成した関数を返します。

def isOdd2 = isEven >=> negate

isOdd(3)
// res7: Writer[Boolean] = Writer(
//   run = (
//     "isEven is called with parameter 3. negate is called with parameter false. ",
//     true
//   )
// )

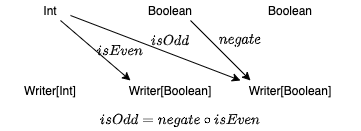
これで、Writer 圏における関数合成を定義できました！

4.2.3 Writer 圏は圏の公理を満たすか

ここで一度、圏が満たすべき性質に立ち戻ってみましょう。1つ目は関数の合成が結合律を満たすこと、2つ目は任意の対象に対して恒等射が存在することでした。

この合成 >=> は、結合律を満たすでしょうか？

タプル (String, A) の各要素に分解して考えてみましょう。1つ目の要素の合成は、 String の連結です。文字列の連結が結合律を満たすのは自明ですね。

2つ目の要素の合成は、標準的な関数合成です。これも結合律を満たしますね。

>=> の内部では文字列の連結と標準的な関数合成をしているだけなので、>=> は結合律を満たします。

恒等射の存在についてはどうでしょうか。実はこれまでの議論に恒等射は出ていないので、新しく定義します。

Writer 圏における恒等射の型は A => Writer[A] ですね。また、恒等射は、とある射と合成するとその射そのものになるような射でした。すなわち、関数 f: A => Writer[B] に対して、恒等射を i: A => Writer[A] とすると、以下の性質が成り立つはずです。

import hamcat.util.Eq.===

def i[A]: A => Writer[A] = ???
def identityLaw1[A, B] = (f[A, B] >=> i[B]) === f[A, B]
def identityLaw2[A, B] = (i[A] >=> f[A, B]) === f[A, B]

そのような関数を pure: A => Writer[A] として定義しましょう。単位律を満たすために、1つ目の要素であるログ文字列はそのまま返し、2つ目の要素である計算結果はそのまま返す関数として実装します。

def pure[A]: A => Writer[A] = a => Writer("" -> a)

pure(1)
// res8: Writer[Int] = Writer(run = ("", 1))
pure(3)
// res9: Writer[Int] = Writer(run = ("", 3))

Writer 圏における射 negate isEven と合成してみましょう。

negate(true)
// res10: Writer[Boolean] = Writer(
//   run = ("negate is called with parameter true. ", false)
// )

(pure >=> negate)(true)
// res11: Writer[Boolean] = Writer(
//   run = ("negate is called with parameter true. ", false)
// )

(negate >=> pure)(true)
// res12: Writer[Boolean] = Writer(
//   run = ("negate is called with parameter true. ", false)
// )

isEven(3)
// res13: Writer[Boolean] = Writer(
//   run = ("isEven is called with parameter 3. ", false)
// )

(pure >=> isEven)(3)
// res14: Writer[Boolean] = Writer(
//   run = ("isEven is called with parameter 3. ", false)
// )

(isEven >=> pure)(3)
// res15: Writer[Boolean] = Writer(
//   run = ("isEven is called with parameter 3. ", false)
// )

合成すると同じ値が返ってくることを確認できましたね。pure は任意の型 A に対して同じ挙動をするので、pure は恒等射です。したがって、Writer 圏は単位律を満たします。

以上のことから、ここで定義した Writer 圏は圏であるといえます (ただし、例で見ているので、厳密に証明していません)。Writer 圏についてまとめると、次の図のようになります。

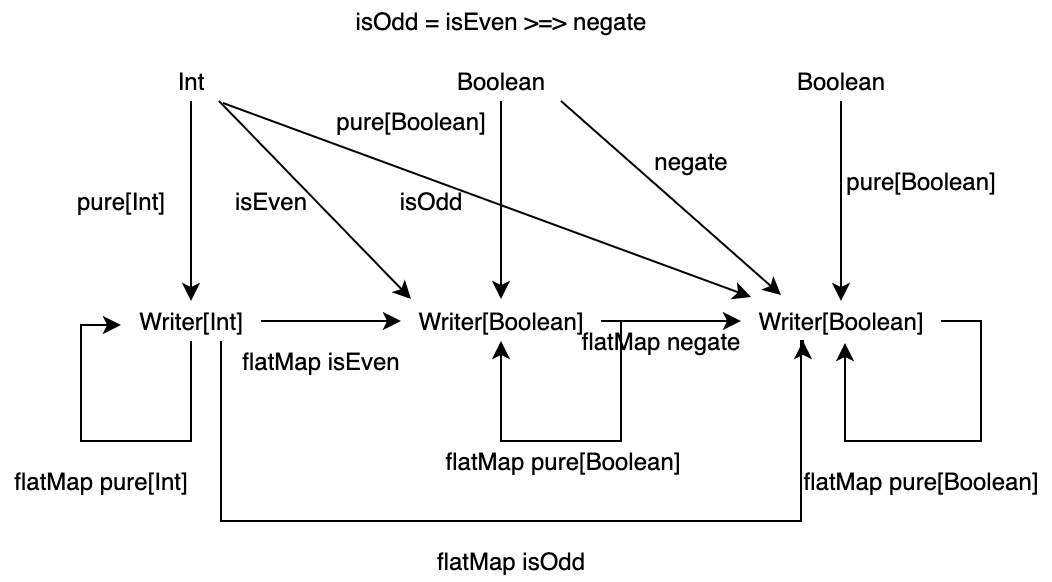
4.2.4 Writer 圏のより一般的な定義

ここで定義した Writer 圏はもう少し抽象的にすることができます。Writer 圏が結合律と単位律を満たすためには、文字列の連結が結合律を満たし、文字列の連結に関する単位元 "" が定義されている必要がありました。つまり、ログを表現する型がモノイド的な性質を満たしていれば、Writer 圏は圏として定義できるはずです。

したがって、型 Writer は、以下のように定義していたものを

case class Writer[A](run: (String, A))

以下のようにパラメータ化して定義できます。

case class Writer[L, A](run: (L, A))

ただし、型 L はモノイドであることが条件です。

これまでの議論を元に、Writer を以下のように定義できます。Writer のデータそのものはタプル (L, A) です。関数を合成するための flatMap メソッド (厳密には >=> ですが)、恒等射の pure メソッドを定義できます。

// Semigroup (半群) は combine だけを持った型クラス
import hamcat.Semigroup
import hamcat.Monoid
import hamcat.syntax.semigroup.*

case class Writer[L, A](run: (L, A)):

  def flatMap[B](f: A => Writer[L, B])(using Semigroup[L]): Writer[L, B] =
    val (log, res) = run
    val (logF, resF) = f(res).run
    Writer((log |+| logF, resF))

object Writer:

  def pure[L, A](a: A)(using m: Monoid[L]): Writer[L, A] = Writer((m.empty, a))

4.3 Kleisli 圏

前節で議論した Writer 圏は、実は Kleisli 圏 (Kleisli category) と呼ばれるものの例です。Kleisli 圏はモナドに基づく圏ですので、厳密な定義はモナドを学んでから見ていきます。

Kleisli 圏では、対象を型、型 A から型 B への射を型 F に対して A => F[B] である関数とします。

case class Kleisli[F[_], A, B](run: A => F[B])

ここで F は自己関手という概念に対応することを後の章で見ていきます。F の例としては List や Option などがあります。それぞれの Kleisli 圏において、射の合成は独自の方法で実装されます。これはまさに1つの自由度であり、ロギングやエラーなどの計算効果に対して表示的意味論を与えることができます。

後の章で、モナドを使って Kleisli 圏を定義します。そのときにまた、本章で述べたことを思い出してもらえると幸いです。

まとめ

関数 f: A => F[B] が圏の公理を満たすよう、射の合成を定義したものが Kleisli 圏である。
Writer 圏は Kleisli 圏の例である。
Writer 圏では、期待する出力 B の他にログ L を出力する関数 f: A => Writer[L, B] を射として考える。
- L は、その射において結合律を満たし、射に関する単位元を持つ必要がある。すなわち、L はモノイドの性質を満たす必要がある。
Writer 圏における射の合成は >=> 演算子として定義された。

4章 Kleisli圏